Other work with the rotating annulus

During my time at AOPP I worked on several projects about the rotating annulus alongside the work on predictability.

Simulated regime diagram and period-doubling bifurcations

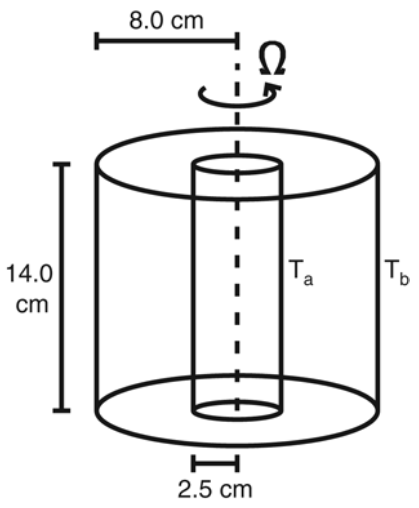
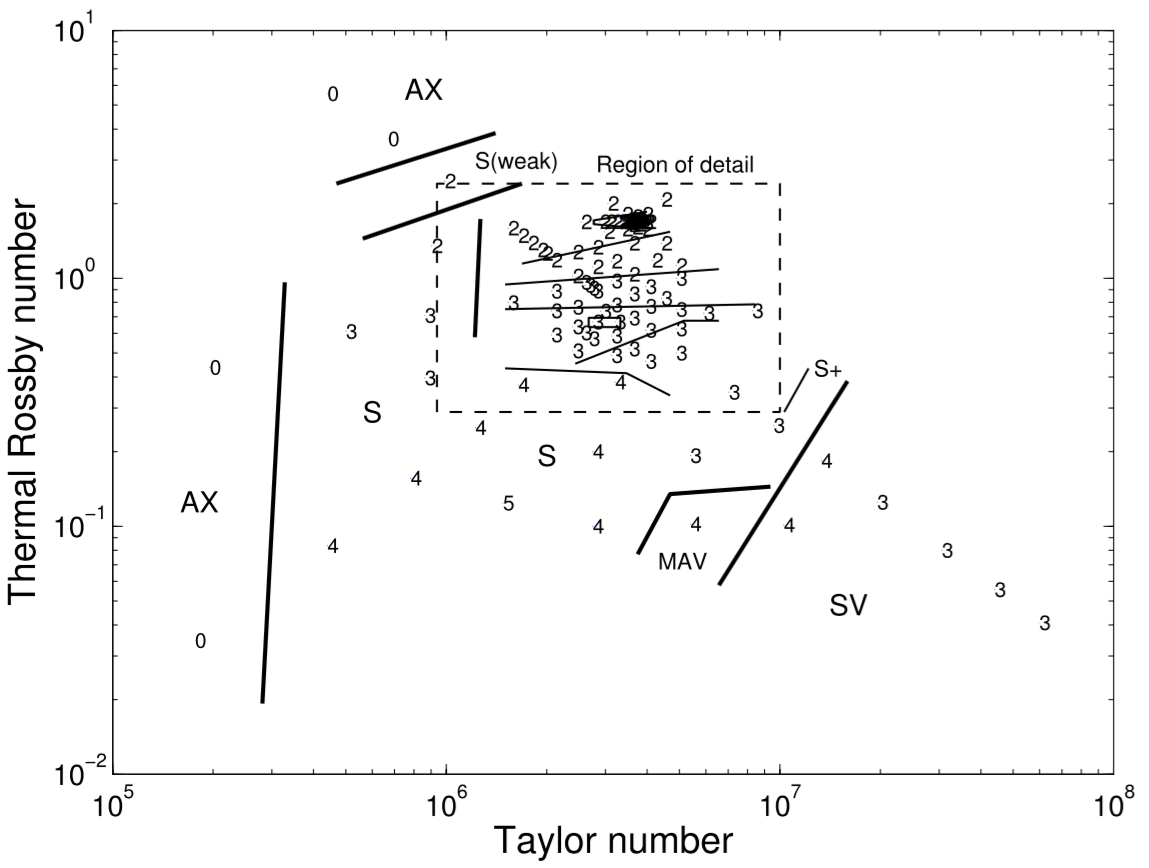
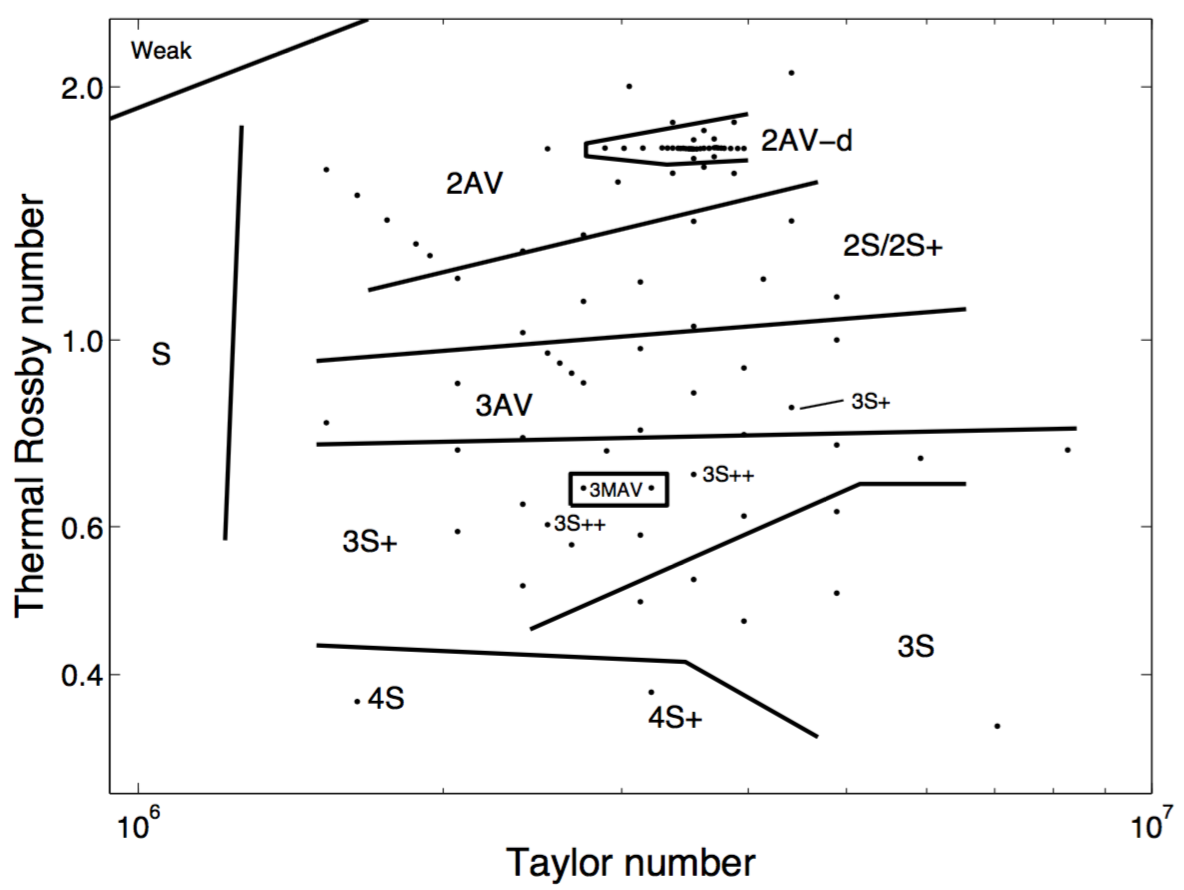
As a precursor to investigating annulus predictability, in Young & Read (2008) we computed a numerical regime diagram for the classical thermally-driven rotating annulus using the MORALS code. Such a diagram classifies the fluid flow as a function of two controlling parameters, the Taylor number and thermal Rossby (Hide) number, which in turn depend on tank rotation rate, temperature difference between the two cylinders, fluid, and tank dimensions. The simulated regime diagram compares well in many respects to the regime diagrams produced from laboratory experiments such as Hide & Mason (1975), Hignett et al. (1985), and others.

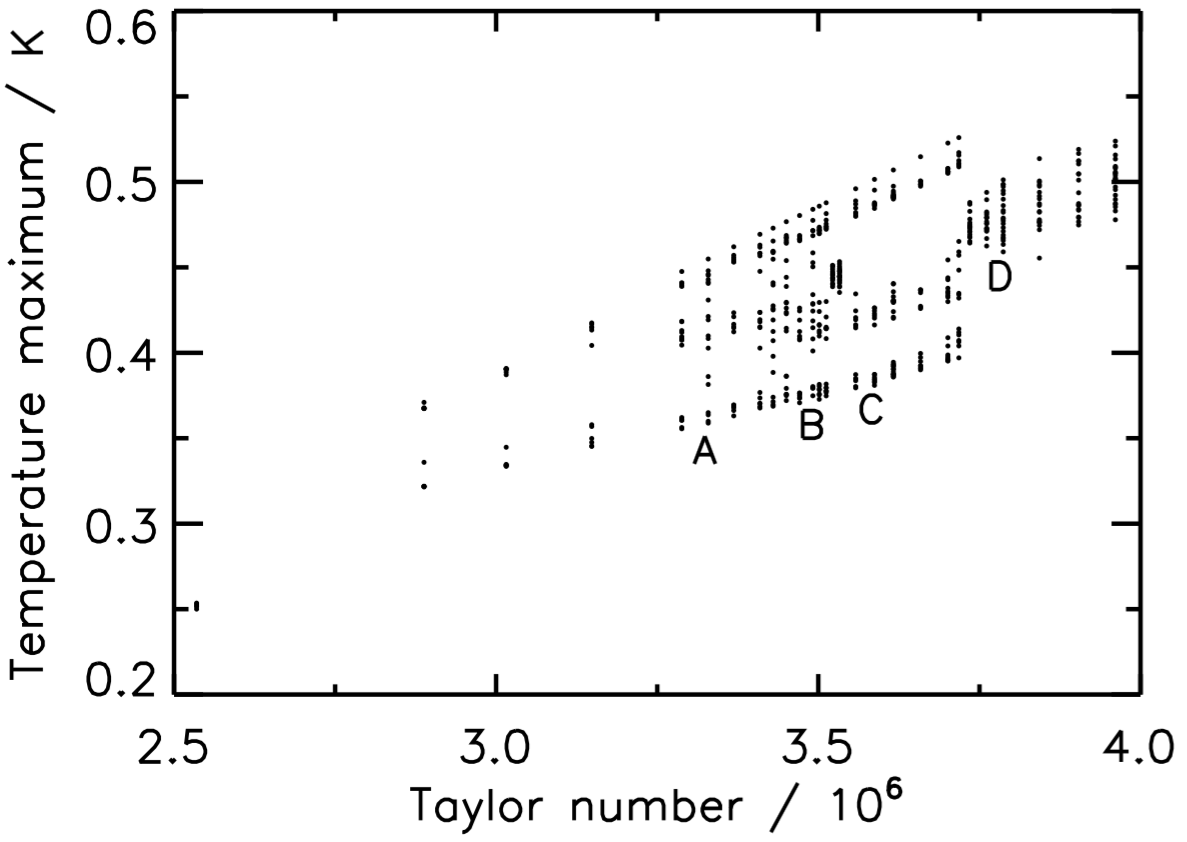
During this work we found a region of the parameter space where there exists a sequence of bifurcations in the flow similar to the bifurcations of the logistic map, with associated regions of parameter space displaying regular and chaotic behaviour. These bifurcations were observed in a sequence of runs at high temperature forcing, were identified by Poincaré sections of the dominant temperature mode amplitude time series, and were verified and classified using return maps and Lyapunov exponents.


Regime diagram for simulated thermally-driven rotating annulus flow (top) and region of detail (bottom). AX: axisymmetric; S(weak): weak, steady wave; S: steady wave; S+/S++: steady wave with weak amplitude vacillation; AV: amplitude vacillation; AV-d: amplitude vacillation with period doubling; MAV: modulated amplitude vacillation; SV: structural vacillation. Numbers show the dominant azimuthal wavenumber. (Young & Read, 2008, erratum).

Bifurcation diagram showing period-doubling and chaos. This shows all the maxima of the wavenumber-2 temperature mode time series for a sequence of simulations along the line of points in the 2AV-d region above, as a function of the Taylor number (moving from left to right on the diagram above). (Young & Read, 2008, erratum).

Generation of inertia-gravity waves by a boundary-layer instability

Waves with shorter periods than the inertial period exist in the atmosphere as inertia-gravity waves and in the oceans as Poincaré and internal gravity waves. Of particular interest are those arising either from local secondary instabilities or from spontaneous emission due to loss of dynamical balance.

In Jacoby et al. (2011) we examined short period waves in the thermally-driven rotating annulus using the MORALS simulation. These waves had properties consistent with inertia-gravity waves generated by a localised instability within the thermal boundary layer, the location of which was determined by regions of strong shear and downwelling at certain points within a large-scale baroclinic wave flow.

The resulting instability launched small-scale inertia-gravity waves into the geostrophic interior of the flow. Such a mechanism has many similarities with those responsible for launching small- and meso-scale inertia-gravity waves in the atmosphere from fronts and local convection.


Horizontal and vertical sections through a rotating annulus simulation showing inertia-gravity waves near the inner boundary. This shows horizontal divergence at mid-height (top) and at a single azimuthal grid point (bottom); frames are separated by 12s (Jacoby et al., 2011).

Temperature time series in the annulus showing inertia-gravity waves. Data are at mid-height / mid-radius. Experimental data are from Read (1992) (Jacoby et al., 2011).

The energy cycle in the rotating annulus

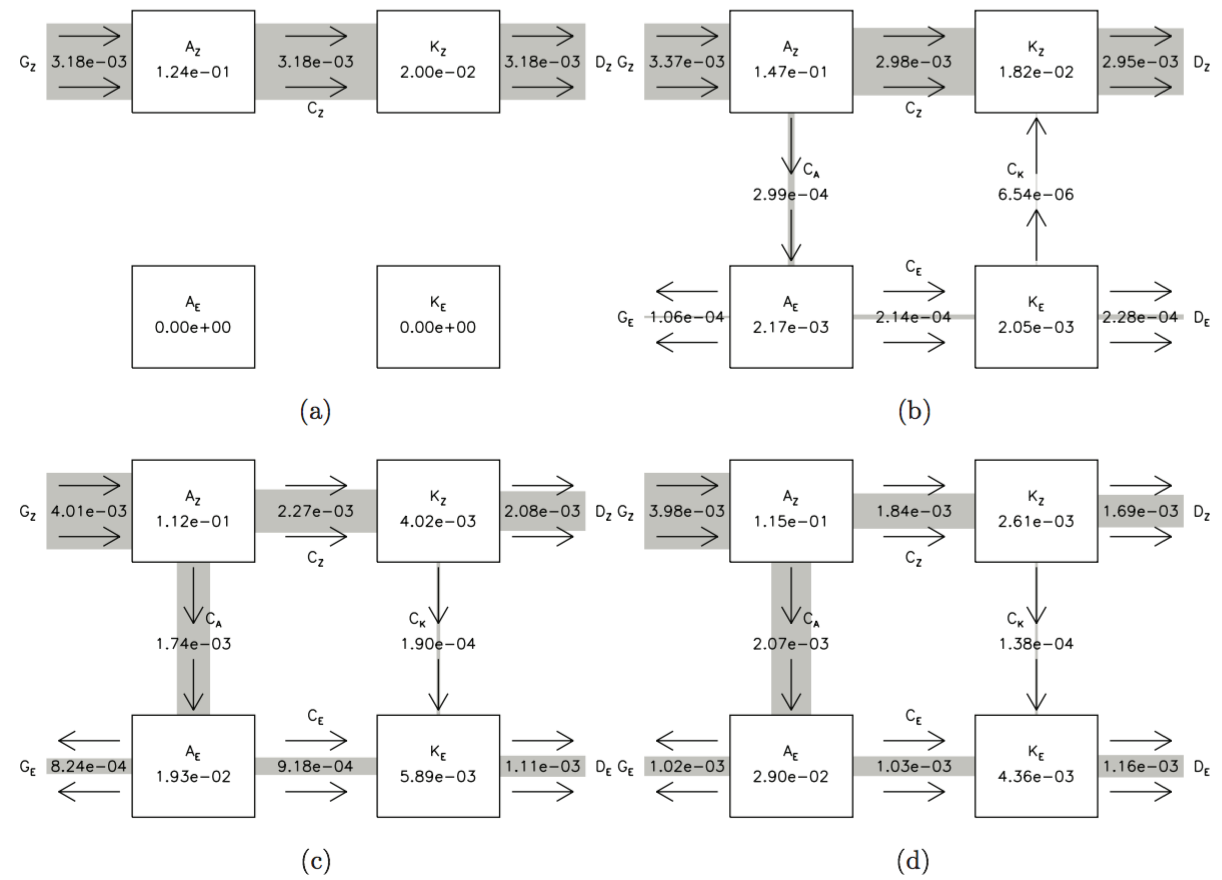
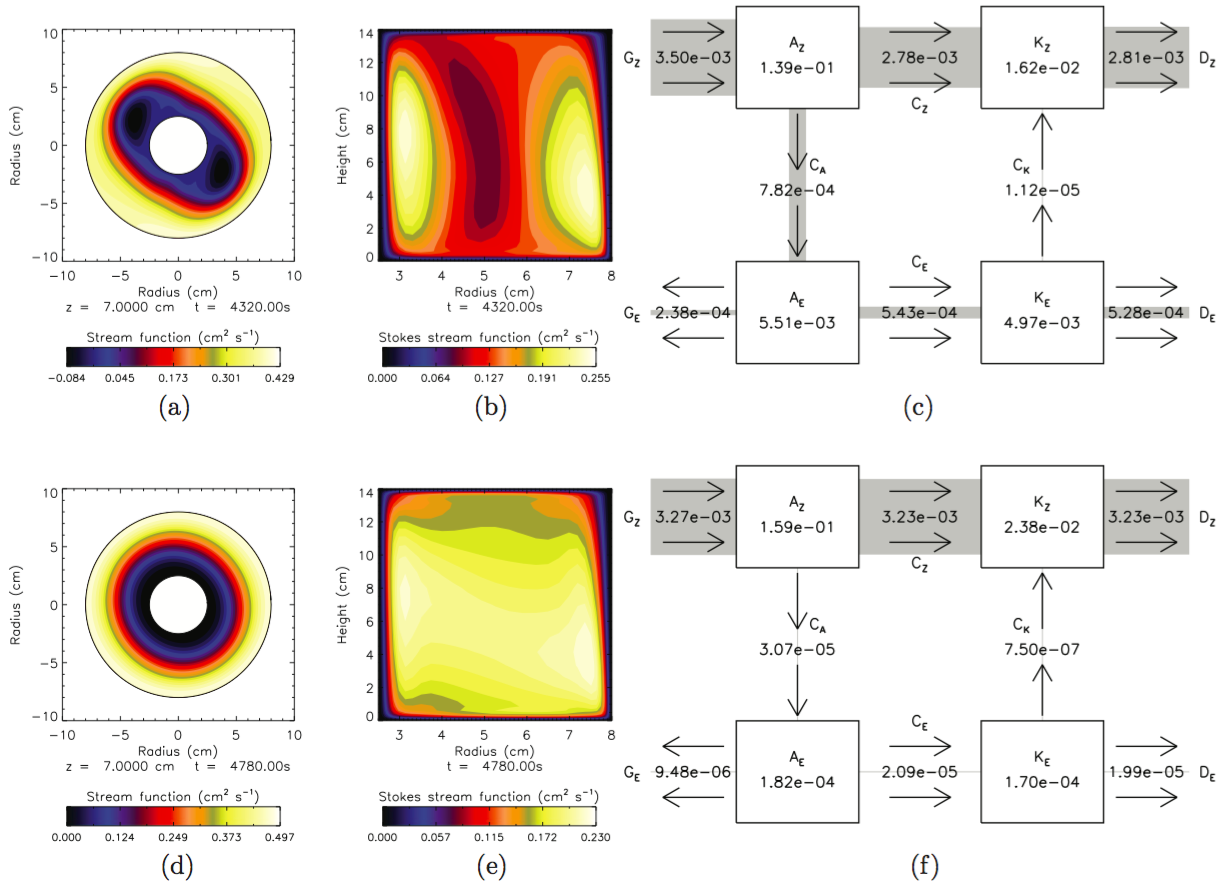
In Young (2014) I investigated the Lorenz cycle in simulations of the main flow regimes found in the thermally-driven rotating annulus.

The primary driver for this work was to develop some code to measure similar diagnostics in another project investigating flow in the rotating annulus using a "tidally locked" configuration, but this is yet to be published.

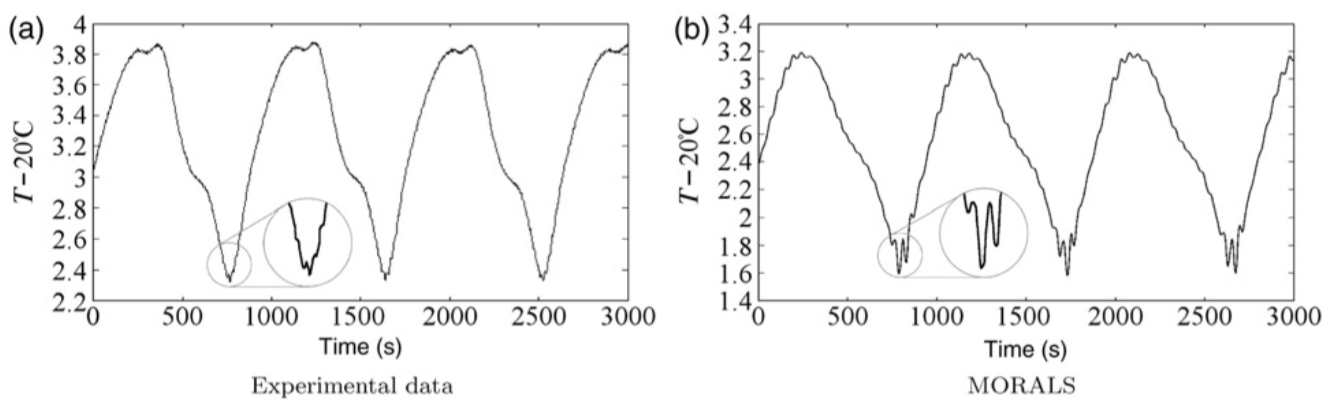
Energy cycles were computed for axisymmetric, steady, amplitude vacillating, and structurally vacillating flow regimes. The simulation allows contributions to the energy diagnostics to be identified in parts of the fluid that cannot be measured in experiments, particularly by filling in the vertical plane. These energy diagnostics and the conversions between them agreed well with experimental time series of kinetic and potential energy in amplitude vacillating flow (Pfeffer et al., 1974).

Two of the three major energy transfer paradigms of the Lorenz energy cycle were identified. A Hadley-cell overturning circulation was found in the axisymmetric regime and at the weak-eddy extreme of the amplitude vacillation cycle. Baroclinic instability was found in the steady and structural vacillation flow regimes, and at the strong-eddy extreme of the amplitude vacillation cycle. The third, barotropic instability, was never dominant, but increased in strength as rotation rate increased.

For structurally vacillating flow, which matches the Earth's thermal Rossby number well, the ratios between energy conversions associated with baroclinic and barotropic instabilities (CA vs CK, and GZ vs CA) were similar to the measured ratios in the Earth’s mid-latitudes (Lorenz, 1955).

Lorenz energy cycles for four rotating annulus flow regimes. (a) axisymmetric flow, (b) amplitude vacillation, wavenumber 2, (c) steady flow, wavenumber 3, (d) structural vacillation, wavenumber 3. All energy reservoirs (boxes) are (10−4 J kg−1) and all energy transfers (arrows) are in (10−4 W kg−1) (Young, 2014).

Lorenz energy cycles at the two extremes of the amplitude vacillation cycle. Top row shows where eddies are strongest, and bottom row where eddies are weakest. All energy reservoirs (boxes) are (10−4 J kg−1) and all energy transfers (arrows) are in (10−4 W kg−1) (Young, 2014).

Simulations of a freely-convecting annulus configuration

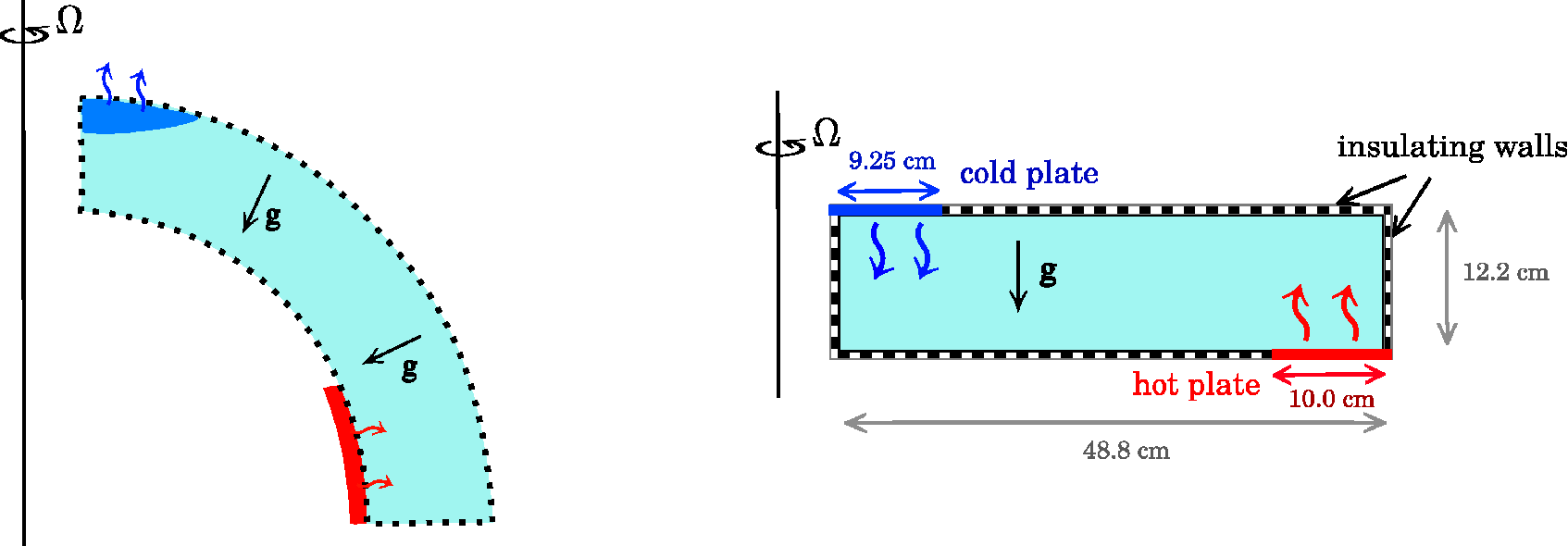
To support the design and construction of a new rotating tank experiment in the AOPP GFD laboratory, described by Scolan & Read (2017), in Wright et al. (2017) we ran a series of axisymmetric simulations using MORALS that reproduced this setup numerically.

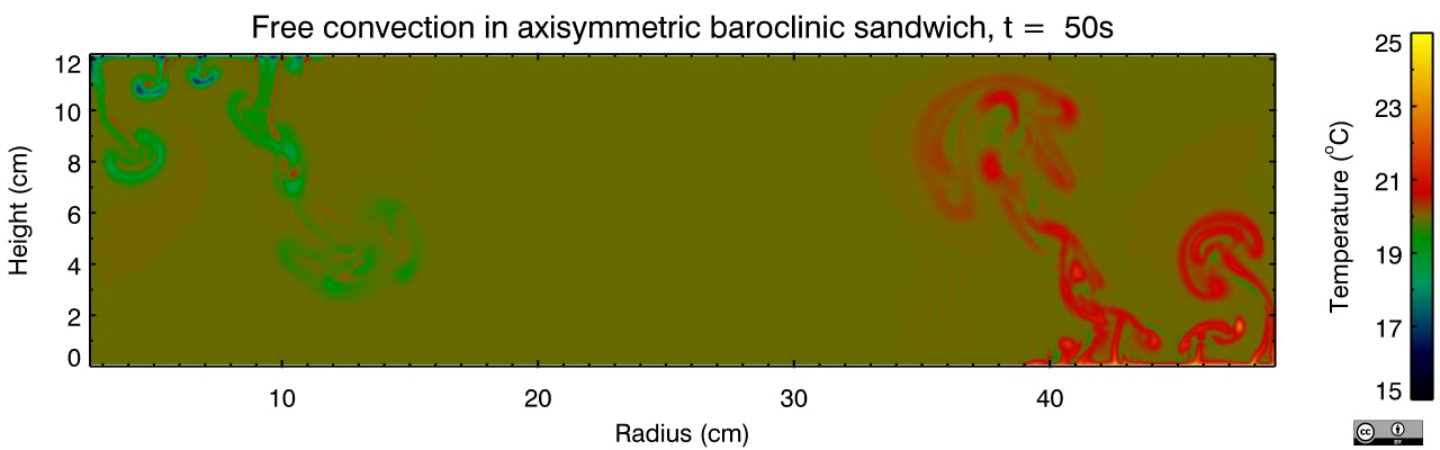
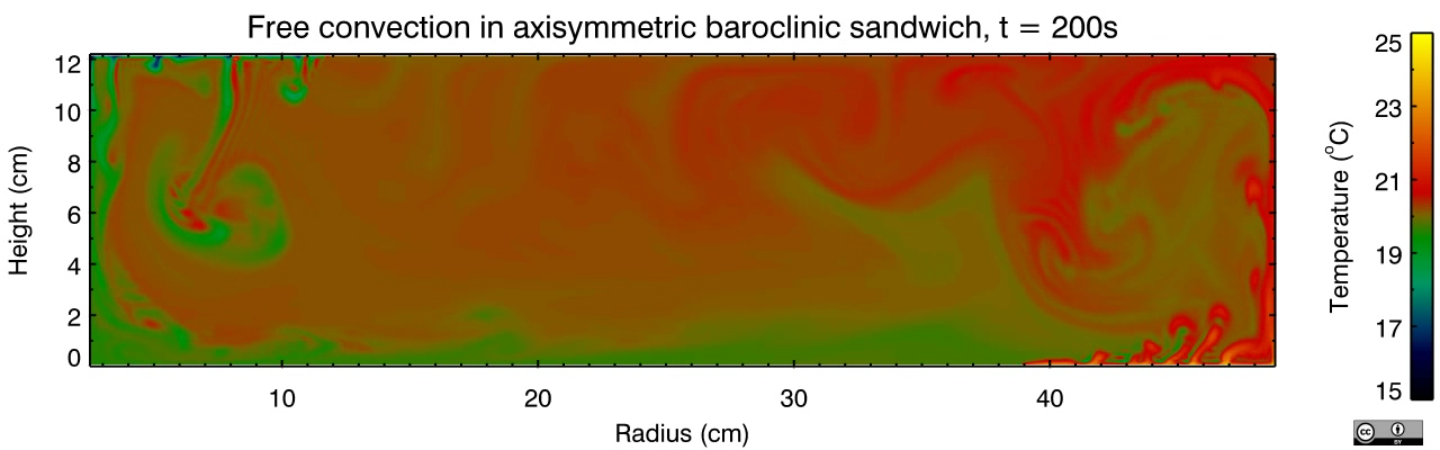
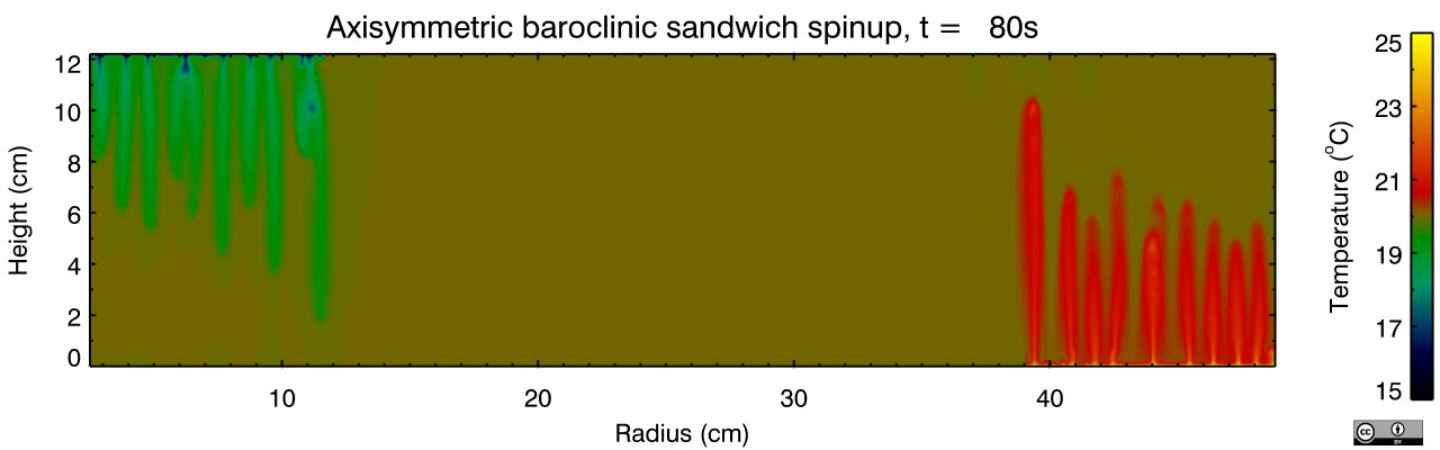
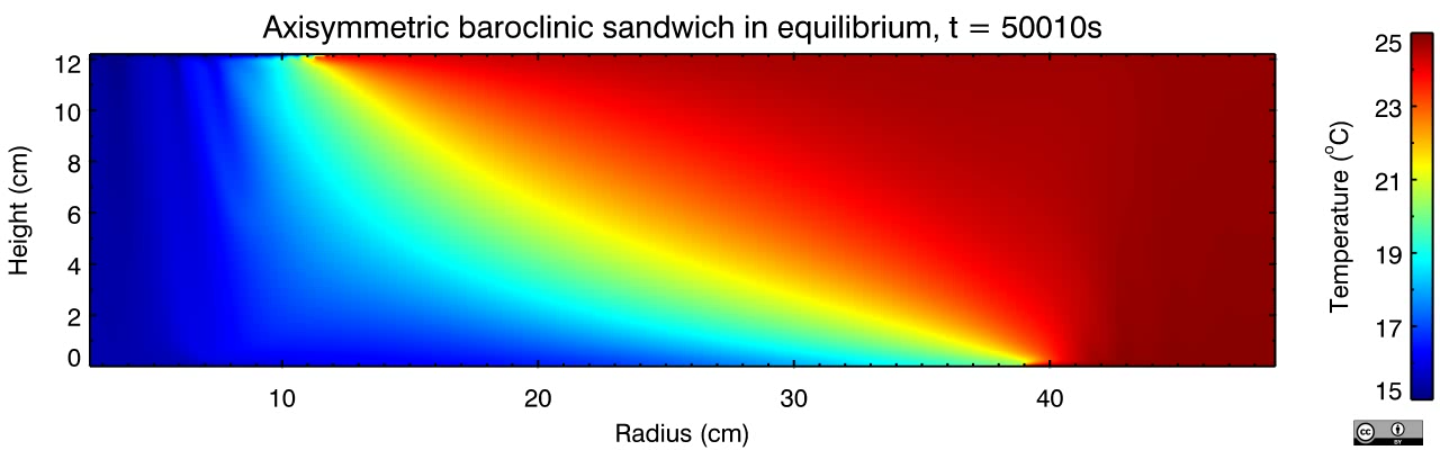
In this experiment, nicknamed the "baroclinic sandwich", convection is driven by a heated annular ring on the outside of the base and a cooled circular disk in the centre of the top surface. This is a variant of the classical thermally-driven annulus, where uniform heating and cooling are applied through the outer and inner sidewalls respectively.

This is a more realistic analogue of a planetary atmosphere as it heats the fluid at the bottom surface and cools it at the top, rather than having a fixed temperature throughout the atmospheric column at different latitudes, as represented by the classical annulus. On Earth, the atmosphere is heated primarily from below by re-emission of longwave radiation from the surface, and is cooled at high altitudes. This heats the lowest levels of the atmosphere, which then drives convection, doing so more vigorously at lower latitudes as there is more solar heating there. This arrangement of thermal forcing in the experiment is expected to result in freely convecting regions in the inner and outer regions of the tank (tropics and polar regions) with a baroclinic zone sandwiched between them (mid-latitude zone).

Schematic of a planetary atmosphere (left) and the laboratory analogue "baroclinic sandwich" experiment (right). (Wright et al., 2017).

We investigated a series of equilibrated, 2D axisymmetric flows across a large region of parameter space. Several distinct flow regimes were identified by rotation rate and differential heating. These regimes were defined as a function of the ratio of the horizontal Ekman layer thickness to the non-rotating thermal boundary layer thickness, and were found to be similar to those identified in previous annulus experiments. Convection without rotation was also considered and the scaling of heat transport with Rayleigh number was calculated. The system's behaviour was found to be aspect ratio dependent, which was apparent in the scaling of the non-rotating Nusselt number and in transitions between flow regimes.

Although comparisons may be drawn with the classical annulus, Rayleigh-Bénard and horizontal convection, the new system does not seem to behave exactly as any of these three. In particular the aspect ratio dependence of both the non-rotating and rotating systems remains unexplained. In the rotating case, the observed aspect ratio dependency of the transitions between regimes suggests that this may be important for the threshold beyond which baroclinic instability develops.


Free convection during spin-up at low rotation rate (0.001 rad s-1) after 50 and 200s. At low rotation rate the convective plumes are unconstrained, leading to characteristic "mushroom" plumes (Wright et al., 2017).

Convection during spin-up at high rotation rate (1 rad s-1). At high rotation rates the convective plumes are almost vertical due to the flow being constrained into Taylor columns. (Wright et al., 2017).

Baroclinic sandwich 2D simulation in equilibrium (1 rad s-1). After a long time the input and output power at the hot and cold plates become balanced. Between the two convective zones the sloping isotherms characteristic of baroclinically unstable flow develop.